-
Measuring and Understanding the Output Voltage Ripple of a Boost Converter
Measuring and Understanding the Output Voltage Ripple of a Boost Converter
Trademarks
All trademarks are the property of their respective owners.
1 Introduction
A boost converter circuit such as TPS61022 is shown in Figure 1-1. With alternate turning on and off of the two integrated MOSFET, the inductor stores energy and then released to VOUT which is higher than the input voltage. The average value of VOUT is set by the FB pin and R1, R2 resistors.
 Figure 1-1 Simplified Schematic of TPS61022
Figure 1-1 Simplified Schematic of TPS61022The ideal operating waveform at heavy loading condition are shown in Figure 1-2. In the image:
- IL is the inductor current.
- IOUT is the output current of the boost converter.
- ID is the current through the synchronous rectification MOSFET.
- SW is voltage waveform in SW pin.
- ΔVOUT is output voltage ripple.
 Figure 1-2 Ideal Operating Waveform of a
Boost
Figure 1-2 Ideal Operating Waveform of a
Boost
In this equation:
- COUT is the effective output capacitance.
- fSW is the switching frequency of the boost.
However, one may observe much larger output voltage ripple than the calculation result in real circuits. This application details the root cause of the observation and proposes solution to solve the problem.
2 Observation in Bench Test
The Equation 1 assumes that the output capacitor is ideal and capacitor ripple is perfectly measured by the voltage probe. However, the actual ripple waveform would be related to the setting of oscilloscope bandwidth and voltage probe grounding method.
The bandwidth of a Tektronix oscilloscope can be set to 20 MHz or full bandwidth, which could be 500 MHz or higher depending on the oscilloscope model. The voltage probe grounding loop could be as in Figure 2-1. The left probe has long grounding wire and the test point is not closed to the capacitor. The right probe has very short grounding wire and the test point is on the terminals of the capacitor.
 Figure 2-1 Setup of Voltage Probe
Figure 2-1 Setup of Voltage ProbeTaking TPS61022 as an example, the output ripple waveform with different setting are shown from Figure 2-2 to Figure 2-4. From the waveform, three conclusions can be derived :
- The loop between the probe tip and its ground must be as small as possible, to avoid any noise coupling.
- In additional to the switching frequency ripple, there is large and high frequency voltage spike across the output capacitor.
- The voltage spike is much small at 20-MHz bandwidth setting as the oscilloscope acts at low pass filter.
 Figure 2-2 Voltage Ripple with Long Ground
Cable and Full Bandwidth
Figure 2-2 Voltage Ripple with Long Ground
Cable and Full Bandwidth Figure 2-3 Voltage Ripple with Short Ground
Cable and Full Bandwidth
Figure 2-3 Voltage Ripple with Short Ground
Cable and Full Bandwidth Figure 2-4 Voltage Ripple with 20-MHz
Bandwidth
Figure 2-4 Voltage Ripple with 20-MHz
Bandwidth3 Root Cause Analysis
The voltage spike shown in Figure 2-3 is caused by the ESR (effective series resistance) and ESL (effective series inductance) of the output capacitor. The Figure 3-1 shows the impedance of a 0805-package ceramic capacitor over frequency. Point A is the resonant frequency of the ESL and the capacitor.
The impedance of the capacitor is equal to its ESR which is approximately 3.5mΩ. The impedance of the capacitor increases linearly once the frequency is higher than 10 MHz. This is behavior of the ESL. From the impedance of point B and point C, the ESL is estimated to be 0.27nH.
 Figure 3-1 Characteristic of a Ceramic
Capacitor
Figure 3-1 Characteristic of a Ceramic
CapacitorThe voltage crossing the ESR is in proportion to the current through capacitor. A ceramic capacitor has only several milliohm resistances and normally there will be several ceramic capacitors in parallel. Thus, this voltage ripple caused by ESR is small and can be neglected.
The voltage crossing the ESL is in proportional to its di/dt, which could be very large. Because the switching frequency of a boost converter always tends to be as large as possible to reduce the solution size. The di/dt will also increase with the switching frequency to reduce the power loss in the IC.
Considering the ESL and the parasitic inductance of the PCB trace and IC package, the schematic of the boost converter power stage is shown in Figure 3-2 where LPAR1 is the sum of pin-out and PCB parasitic inductor and LPAR2 is the parasitic inductor of the GND pin;
 Figure 3-2 Boost Converter Power Stage With Parasitic Inductor
Figure 3-2 Boost Converter Power Stage With Parasitic InductorWhen Q1 turns off and SW node voltage is higher than VOUT, the inductor current starts to transit from Q1 to Q2. During the current transition period, the equivalent circuit is shown in Figure 3-3, where
- CQ1 represents parasitic capacitor of Q1. The turning-off time of Q1 is neglected.
- IL1 represents the inductor as inductor current is almost constant during the short transition period.
- VCOUT represent the voltage in the ideal capacitance portion of the output capacitor. the voltage is almost constant during this transition period.
 Figure 3-3 Simplified Model at Low Side MOSFET Turning Off
Figure 3-3 Simplified Model at Low Side MOSFET Turning OffThe Figure 3-3 can be further simplified to a LC circuit with initial inductor current IL1. The inductor value is the sum of all the parasitics inductor in the circuit. The capacitor is CQ1. So the voltage spike of the ESL is defined by Equation 2. The voltage spike is in proportinal to inductor current.
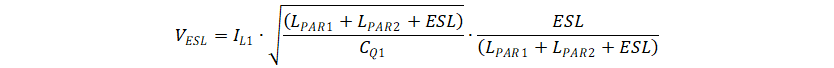
And the oscillation frequency is defined by Equation 3.
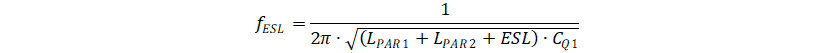
When Q1 turns on, the inductor current firstly transits from Q2 to Q1, then voltage Q1 quickly declines to zero. The simplified schematic during this period is shown in Figure 10, where CQ2 represents the parasitic capacitance of Q2 when it turns off.
 Figure 3-4 Simplified Model at Low Side MOSFET Turning On
Figure 3-4 Simplified Model at Low Side MOSFET Turning OnThe maximum voltage spike at ESL is defined by Equation 4. The circuit can also be simplified to a LC circuit. The VESL voltage level is in proportion to the boost output voltage, and the oscillation frequency is the same as Equation 3 because the CQ2 and CQ1 is similar.
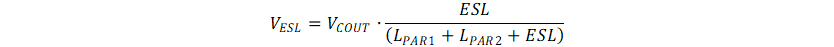
Taking TPS61022EVM as example, CQ1 and CQ2 are approximately 0.4 nF. LPAR1 is closed to 0.3 nH; LPAR2 is approximately 0.05 nH; ESL is approximately 0.09 nF as there are three capacitors in parallel. Thus, the LC oscillation frequency is up to 300 MHz.
At VIN=3.6V, VOUT=5V, IOUT=3A condition, the IL1 is about 4.4 A. The VESL spike at both Q1 turning on and turning off condition are approximately 0.75 V. however, the actual voltage spike from Figure 2-3 is lower than this calculation result, especially at Q1 turning-on condition. The main factor leading to the gap is the turning on/off time of the Q1. The turning on/off time of Q1 is at 5ns level. The greatly impacts the voltage spike caused by a 300-MHz LC ringing. It is hard to have an equation to calculate the voltage spike if considering the turning on/off time. A better method is simulation with PSPICE-FOR-TI or other tools.
4 A Simple Solution
The actual output ripple in real system circuit is not always equal to the value measured in the EVM. And this high frequency noise doesn’t always impact the system loading:
- If there is an LDO between the boost output and the loading, The LDO and its input and output capacitor would help to filter such high frequency noise.
- If there is long cable between the boost output and the loading, the ESR, ESL of the cable and the bypass capacitor closed to the loading forms RLC filter to reduce the high frequency noise.
- Such high frequency noise may not impact the performance the system loading.
But if the loading is sensitive to the high frequency noise, or EMI performance is critical to system, a ferrite bead with high impedance at high frequency can greatly reduce such noise. The location of the ferrite bead is shown in Figure 4-1. The impedance of the FB should be much higher than COUT2 at frequency closed to 300 MHz.
 Figure 4-1 Location of the Bead
Figure 4-1 Location of the BeadTaking BLM18KG30TH1 as an example, its impedance is higher than 35Ω at frequency from 200 MHz to 1000 MHz. the impedance is much higher than a capacitor as in Figure 4-2.
 Figure 4-2 Characteristic of a Bead
Figure 4-2 Characteristic of a BeadAfter adding ferrite bead and moving one of three capacitors to location COUT2 in the TPS61022EVM, The output voltage ripple is shown in Figure 4-3. The high frequency noise is greatly reduced and the ripple is mainly the switching frequency ripple.
 Figure 4-3 Output Voltage Ripple With a
Bead
Figure 4-3 Output Voltage Ripple With a
Bead