SLUAAO2 March 2023 CSD13201W10 , CSD13202Q2 , CSD13302W , CSD13303W1015 , CSD13306W , CSD13380F3 , CSD13381F4 , CSD13383F4 , CSD13385F5 , CSD15380F3 , CSD15571Q2 , CSD16301Q2 , CSD16321Q5 , CSD16322Q5 , CSD16323Q3 , CSD16325Q5 , CSD16327Q3 , CSD16340Q3 , CSD16342Q5A , CSD16401Q5 , CSD16403Q5A , CSD16404Q5A , CSD16406Q3 , CSD16407Q5 , CSD16408Q5 , CSD16409Q3 , CSD16410Q5A , CSD16411Q3 , CSD16412Q5A , CSD16413Q5A , CSD16414Q5 , CSD16415Q5 , CSD16556Q5B , CSD16570Q5B , CSD17301Q5A , CSD17302Q5A , CSD17303Q5 , CSD17304Q3 , CSD17305Q5A , CSD17306Q5A , CSD17307Q5A , CSD17308Q3 , CSD17309Q3 , CSD17310Q5A , CSD17311Q5 , CSD17312Q5 , CSD17313Q2 , CSD17318Q2 , CSD17322Q5A , CSD17327Q5A , CSD17381F4 , CSD17382F4 , CSD17483F4 , CSD17484F4 , CSD17501Q5A , CSD17505Q5A , CSD17506Q5A , CSD17507Q5A , CSD17510Q5A , CSD17522Q5A , CSD17527Q5A , CSD17551Q3A , CSD17551Q5A , CSD17552Q3A , CSD17552Q5A , CSD17553Q5A , CSD17555Q5A , CSD17556Q5B , CSD17559Q5 , CSD17570Q5B , CSD17571Q2 , CSD17573Q5B , CSD17575Q3 , CSD17576Q5B , CSD17577Q3A , CSD17577Q5A , CSD17578Q3A , CSD17578Q5A , CSD17579Q3A , CSD17579Q5A , CSD17581Q3A , CSD17581Q5A , CSD17585F5 , CSD18501Q5A , CSD18502KCS , CSD18502Q5B , CSD18503KCS , CSD18503Q5A , CSD18504KCS , CSD18504Q5A , CSD18509Q5B , CSD18510KCS , CSD18510KTT , CSD18510Q5B , CSD18511KCS , CSD18511KTT , CSD18511Q5A , CSD18512Q5B , CSD18513Q5A , CSD18514Q5A , CSD18531Q5A , CSD18532KCS , CSD18532NQ5B , CSD18532Q5B , CSD18533KCS , CSD18533Q5A , CSD18534KCS , CSD18534Q5A , CSD18535KCS , CSD18535KTT , CSD18536KCS , CSD18536KTT , CSD18537NKCS , CSD18537NQ5A , CSD18540Q5B , CSD18541F5 , CSD18542KCS , CSD18542KTT , CSD18543Q3A , CSD18563Q5A , CSD19501KCS , CSD19502Q5B , CSD19503KCS , CSD19505KCS , CSD19505KTT , CSD19506KCS , CSD19506KTT , CSD19531KCS , CSD19531Q5A , CSD19532KTT , CSD19532Q5B , CSD19533KCS , CSD19533Q5A , CSD19534KCS , CSD19534Q5A , CSD19535KCS , CSD19535KTT , CSD19536KCS , CSD19536KTT , CSD19537Q3 , CSD19538Q2 , CSD19538Q3A , CSD22202W15 , CSD22204W , CSD22205L , CSD22206W , CSD23202W10 , CSD23203W , CSD23280F3 , CSD23285F5 , CSD23381F4 , CSD23382F4 , CSD25202W15 , CSD25211W1015 , CSD25213W10 , CSD25304W1015 , CSD25310Q2 , CSD25402Q3A , CSD25404Q3 , CSD25480F3 , CSD25481F4 , CSD25483F4 , CSD25484F4 , CSD25485F5 , CSD25501F3 , CSD75207W15 , CSD75208W1015 , CSD83325L , CSD85301Q2 , CSD85302L , CSD85312Q3E , CSD86311W1723 , CSD87312Q3E , CSD87313DMS , CSD87501L , CSD87502Q2 , CSD87503Q3E , CSD88537ND , CSD88539ND

7 Estimating SOA for Non-Square Waveforms

What if the waveforms are not square? TI performs SOA testing to destruction using square waveforms as shown in Figure 7-1.

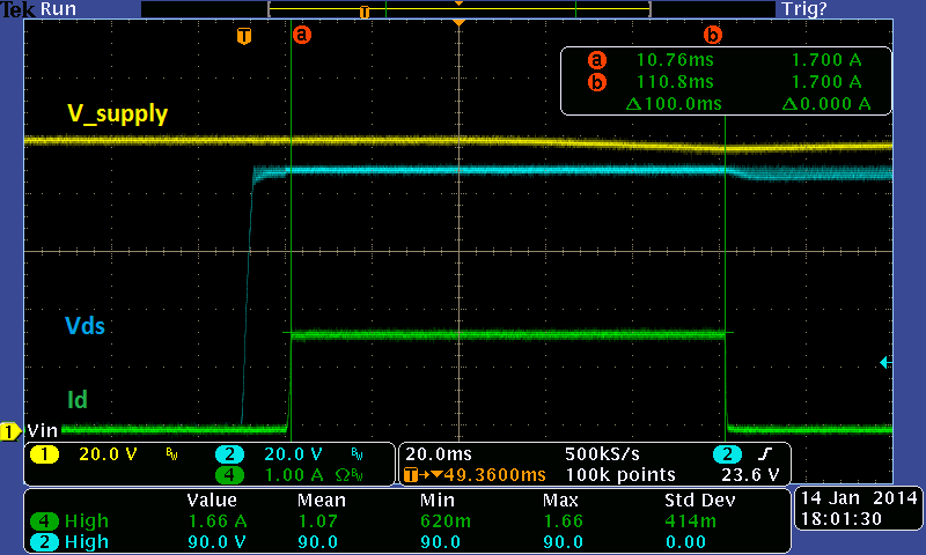Figure 7-1 Typical SOA Test Waveform

In section 2.3.3 of the above mentioned application report, Robust Hot Swap Design, a method is presented for approximating the MOSFET stress as a square pulse with equivalent energy and pulse width as follows:

Equation 11.

E_{1} = E_{2} = \int_{0}^{t_{1}} v_{D S} (t) \times i_{D S} (t) d t

Equation 12.

t_{2} = \frac{E_{2}}{P_{M A X}}

In many applications, one of the waveforms is a linear ramp while the other is held constant. For example, in a hot swap circuit during inrush, V_DS is ramping down while I_DS is constant as shown in Figure 7-2.

Figure 7-2 Hot Swap Inrush Example Waveform

For this example, assume V_DS decays linearly from 12 V down to 0 V in 20 ms while I_DS = 6 A. The energy, E₁, in the pink shaded area under the power curve is calculated as follows:

Equation 13.

E_{1} = \int_{0}^{t_{1}} v_{D S} (t) \times i_{D S} (t) d t

Equation 14.

v_{D S} (t) = V_{D S} \times (1 - \frac{t}{t_{1}})

Equation 15.

i_{D S} (t) = I_{D S}

Equation 16.

E_{1} = V_{D S} \times I_{D S} \int_{0}^{t_{1}} (1 - \frac{t}{t_{1}}) d t = \frac{V_{D S} \times I_{D S} \times t_{1}}{2}

For the equivalent square pulse, the energy in the blue shaded area is assumed to be equal and the power P₂ is the same as the maximum power in the non-square pulse.

Equation 17.

{E_{1} = E}_{2} = P_{M A X} \times t_{2}

Equation 18.

t_{2} = \frac{E_{2}}{P_{M A X}} = \frac{\frac{V_{D S} \times I_{D S} \times t_{1}}{2}}{V_{D S} \times I_{D S}} = \frac{t_{1}}{2}

Inserting the values from the example:

Equation 19.

V_{D S} = 12 V

Equation 20.

I_{D S} = 6 A

Equation 21.

t_{1} = 20 m s

Equation 22.

P_{M A X} = V_{D S} \times I_{D S} = 12 V \times 6 A = 72 W

Equation 23.

t_{2} = \frac{t_{1}}{2} = \frac{20 m s}{2} = 10 m s

Next, go back and confirm that the equivalent square pulse, V_DS = 12 V and I_DS = 6 A is below the 10 ms curve on the CSD17570Q5B SOA curve as shown in Figure 7-3.

Figure 7-3 SOA Inrush Example

This methodology can be extended for use with other types of pulses including non-monotonic, exponential, constant power, and so on.