SLVK047A May 2020 – November 2022 ADC08D1520QML-SP , ADC10D1000QML-SP , ADC12D1600QML-SP , ADC12D1620QML-SP , ADC12DJ3200QML-SP , ADC14155QML-SP , ADS1278-SP , ADS1282-SP , ADS5400-SP , ADS5424-SP , ADS5444-SP , ADS5463-SP , ADS5474-SP , AM26LS33A-SP , CDCLVP111-SP , CDCM7005-SP , DAC121S101QML-SP , DAC5670-SP , DAC5675A-SP , DP83561-SP , DS16F95QML-SP , DS26F31MQML-SP , DS26F32MQML-SP , DS90C031QML-SP , DS90C032QML-SP , DS90LV031AQML-SP , DS90LV032AQML-SP , DS96F174MQML-SP , DS96F175MQML-SP , INA901-SP , LF198JAN-SP , LF198QML-SP , LF411QML-SP , LM101AQML-SP , LM111QML-SP , LM117HVQML-SP , LM117QML-SP , LM119QML-SP , LM124-SP , LM124AQML-SP , LM136A-2.5QML-SP , LM137JAN-SP , LM137QML-SP , LM139-SP , LM139AQML-SP , LM148JAN-SP , LM158QML-SP , LM185-1.2QML-SP , LM185-2.5QML-SP , LM193QML-SP , LM2940QML-SP , LM2941QML-SP , LM4050QML-SP , LM6172QML-SP , LM7171QML-SP , LM723JAN-SP , LM98640QML-SP , LMH5401-SP , LMH6628QML-SP , LMH6702QML-SP , LMH6715QML-SP , LMK04832-SP , LMP2012QML-SP , LMP7704-SP , LMX2615-SP , LP2953QML-SP , MSP430FR5969-SP , OPA4277-SP , SE555-SP , SMJ320C6701-SP , SMV320C6727B-SP , SMV512K32-SP , SN54AC00-SP , SN54AC02-SP , SN54AC14-SP , SN54AC244-SP , SN54AC245-SP , SN54AC373-SP , SN54AC74-SP , SN54ACT04-SP , SN54ACT244-SP , SN54ACT245-SP , SN54ACT373-SP , SN54ACT374-SP , SN54AHC244-SP , SN54AHC245-SP , SN54AHCT08-SP , SN54AHCT14-SP , SN54ALS244C-SP , SN54HC00-SP , SN54HC02-SP , SN54HC04-SP , SN54HC08-SP , SN54HC10-SP , SN54HC109-SP , SN54HC11-SP , SN54HC132-SP , SN54HC138-SP , SN54HC139-SP , SN54HC14-SP , SN54HC153-SP , SN54HC157-SP , SN54HC161-SP , SN54HC164-SP , SN54HC166-SP , SN54HC20-SP , SN54HC244-SP , SN54HC245-SP , SN54HC273-SP , SN54HC32-SP , SN54HC373-SP , SN54HC374-SP , SN54HC573A-SP , SN54HC595-SP , SN54HC74-SP , SN54HCT04-SP , SN54HCT244-SP , SN54HCT245-SP , SN54HCT373-SP , SN54LS00-SP , SN54LS02-SP , SN54LS04-SP , SN54LS08-SP , SN54LS10-SP , SN54LS123-SP , SN54LS138-SP , SN54LS139A-SP , SN54LS14-SP , SN54LS145-SP , SN54LS161A-SP , SN54LS164-SP , SN54LS165A-SP , SN54LS193-SP , SN54LS240-SP , SN54LS244-SP , SN54LS245-SP , SN54LS26-SP , SN54LS273-SP , SN54LS283-SP , SN54LS32-SP , SN54LS373-SP , SN54LS393-SP , SN54LS74A-SP , SN54LVC00A-SP , SN54LVC138A-SP , SN54LVC14A-SP , SN54LVC646A-SP , SN54LVC74A-SP , SN54LVCH244A-SP , SN54LVCH245A-SP , SN54LVTH162244-SP , SN54LVTH162245-SP , SN54LVTH162373-SP , SN54LVTH162374-SP , SN54LVTH16244A-SP , SN54LVTH16245A-SP , SN54LVTH244A-SP , SN54LVTH245A-SP , SN54LVTH574-SP , SN55182-SP , SN55183-SP , SN55HVD233-SP , SN55LVCP22-SP , SN55LVCP22A-SP , SN55LVDS31-SP , SN55LVDS32-SP , SN55LVDS33-SP , THS4304-SP , THS4511-SP , THS4513-SP , TL1431-SP , TLC2201-SP , TLK2711-SP , TPS50601-SP , TPS50601A-SP , TPS7A4501-SP , TPS7H1101-SP , TPS7H1101A-SP , TPS7H1111-SP , TPS7H2201-SP , TPS7H2211-SP , TPS7H3301-SP , TPS7H4001-SP , TPS7H4002-SP , TPS7H5001-SP , TPS7H5002-SP , TPS7H5003-SP , TPS7H5004-SP , TPS7H6003-SP , TRF0206-SP , UC1525B-SP , UC1611-SP , UC1625-SP , UC1637-SP , UC1705-SP , UC1707-SP , UC1708-SP , UC1709-SP , UC1710-SP , UC1715-SP , UC1823A-SP , UC1825-SP , UC1825A-SP , UC1825B-SP , UC1832-SP , UC1834-SP , UC1842-SP , UC1842A-SP , UC1843-SP , UC1843A-SP , UC1843B-SP , UC1844-SP , UC1844A-SP , UC1845-SP , UC1845A-SP , UC1846-SP , UC1856-SP , UC1863-SP , UC1875-SP , UC1901-SP , UC19432-SP , UCC1806-SP
1 Introduction
Determining the SEE cross-section of robustly radiation-hardened devices becomes more difficult since often few, or possibly even no events are observed during an entire exposure. Determining the cross-section using an average event rate with standard deviation is no longer a viable option, and the common practice of assuming a single error occurred at the conclusion of a null-result can end up in a greatly underestimated cross-section.
In cases where observed events are rare or non-existent, the use of confidence intervals and the Chi-Squared distribution is indicated. The Chi-Squared distribution is particularly well-suited for determining a reliability level when the events occur at a constant rate. In the case of SEE testing where the ion events are random in time and position within the irradiation area, it is expected that the event rate is independent of time (presuming that parametric shifts induced by the total ionizing dose do not affect the failure rate), so the use of Chi-Squared statistical techniques is valid (since events are rare an exponential or Poisson distribution is usually used).
In a typical SEE experiment, the device-under-test (DUT) is exposed to a known, fixed fluence (ions/cm2) while the DUT is monitored for events. This is analogous to fixed-time reliability testing and, more specifically, time-terminated testing, where the reliability test is terminated after a fixed amount of time whether or not a failure has occurred (in the case of SEE tests, fluence is substituted for time and hence it is a fixed fluence test) [1]. Calculating a confidence interval specifically provides a range of values which is likely to contain the parameter of interest (the actual number of events/fluence). Confidence intervals are constructed at a specific confidence level. For example, a 95% confidence level implies that if a given number of units was sampled numerous times and a confidence interval was estimated for each test, the resulting set of confidence intervals would bracket the true population parameter in about 95% of the cases.
To estimate the cross-section from a null-result (no events observed for a given fluence) with a confidence interval, start with the standard reliability determination of lower-bound (minimum) mean-time-to-failure for fixed-time testing (an exponential distribution is assumed):
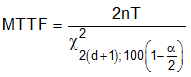
where
- MTTF is the minimum (lower-bound) mean-time-to-failure
- n is the number of units tested (presuming each unit is tested under identical conditions)
- T is the test time
- x2 is the chi-square distribution evaluated at 100(1 – α / 2) confidence level
- d is the degrees-of-freedom (the number of events observed)
With slight modification for this purpose, invert the inequality and substitute F (fluence) in the place of T:
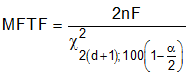
where
- MFTF is mean-fluence-to-failure
- F is the test fluence
- x2 is the chi-square distribution evaluated at 100(1 – α / 2) confidence
- d is the degrees-of-freedom (the number of failures observed)
The inverse relation between MTTF and event rate is mirrored with the MFTF. Thus the upper-bound cross section is obtained by inverting the MFTF:
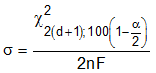
Assume that all tests are terminated at a total fluence of 106 ions/cm2. Also assume that you have a number of devices with very different performances that are tested under identical conditions. Assume a 95% confidence level (σ = 0.05). Note that as d increases from zero events to 100 events, the actual confidence interval becomes smaller, indicating that the range of values of the true value of the population parameter (in this case, the cross section) is approaching the mean value + 1 standard deviation. This makes sense when you consider that as more events are observed, the statistics are improved such that uncertainty in the actual device performance is reduced.
| DEGREES-OF-FREEDOM (d) | 2(d + 1) | χ2 @ 95% | CALCULATED CROSS SECTION (cm2) | ||
|---|---|---|---|---|---|
| UPPER-BOUND @ 95% CONFIDENCE | MEAN | AVERAGE + STANDARD DEVIATION | |||
| 0 | 2 | 7.38 | 3.69E–06 | 0.00E+00 | 0.00E+00 |
| 1 | 4 | 11.14 | 5.57E–06 | 1.00E–06 | 2.00E–06 |
| 2 | 6 | 14.45 | 7.22E–06 | 2.00E–06 | 3.41E–06 |
| 3 | 8 | 17.53 | 8.77E–06 | 3.00E–06 | 4.73E–06 |
| 4 | 10 | 20.48 | 1.02E–05 | 4.00E–06 | 6.00E–06 |
| 5 | 12 | 23.34 | 1.17E–05 | 5.00E–06 | 7.24E–06 |
| 10 | 22 | 36.78 | 1.84E–05 | 1.00E–05 | 1.32E–05 |
| 50 | 102 | 131.84 | 6.59E–05 | 5.00E–05 | 5.71E–05 |
| 100 | 202 | 243.25 | 1.22E–04 | 1.00E–04 | 1.10E–04 |